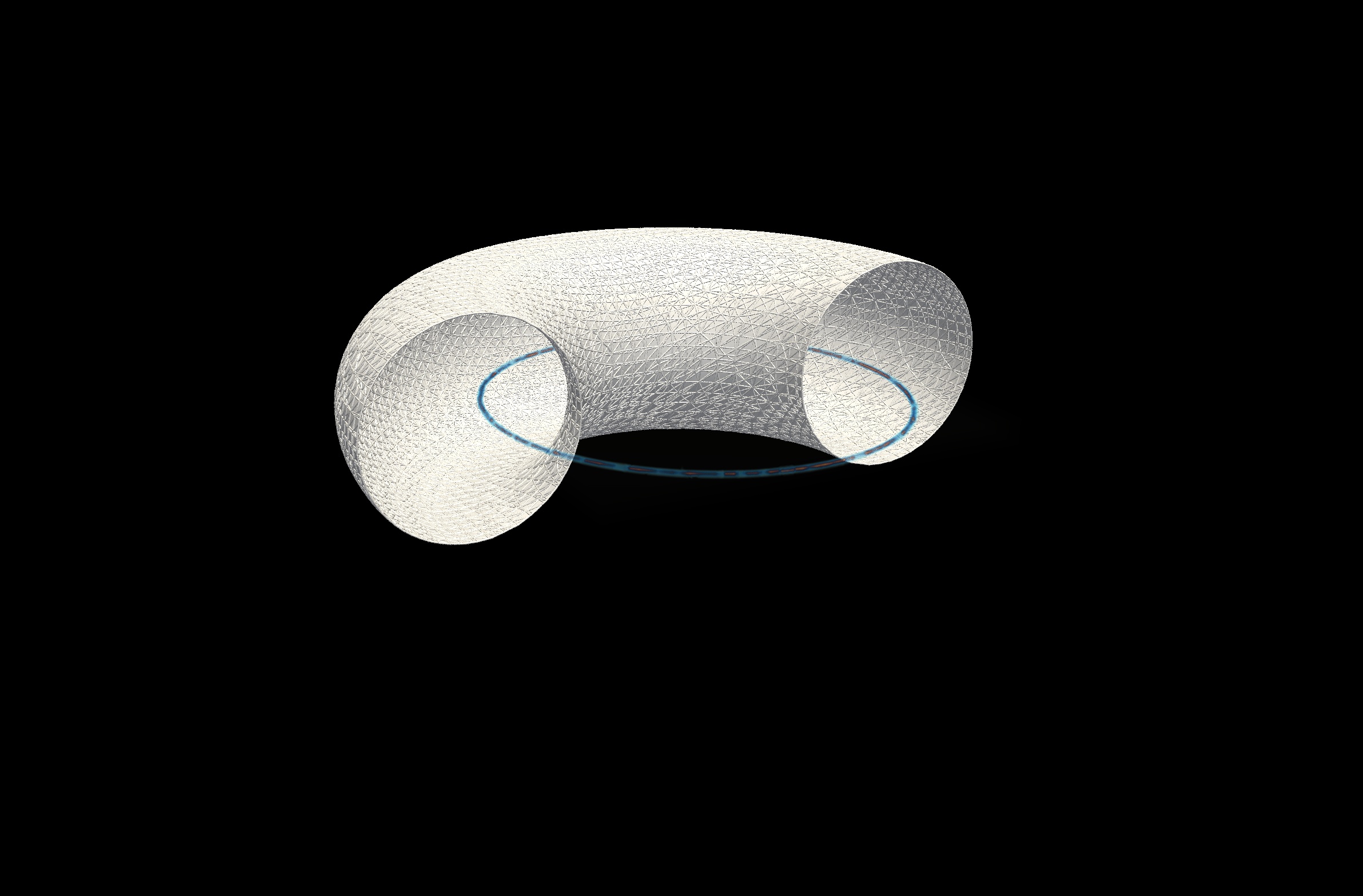
In the new paper Cosmic String and Black Hole Limits of Toroidal Vlasov Bodies in General Relativity by Ames, Andréasson and Logg, we study numerical solutions of the Einstein-Vlasov system modeling a self-gravitating system such as a galaxy. The model is constructed by taking the Einstein field equations of general relativity,
\(
R_{ab} – \frac{1}{2} R g_{ab} = \frac{8\pi G}{c^4} T_{ab},
\)
and modeling the right-hand side stress-energy tensor as a collisionless gas (kinetic model). In this model, a collection of particles are described by a distribution function \(f = f(t, x, p)\) counting the density of particles at time \(t\) at position \(x\) with (four-)momentum \(p\).
We make some simplifying assumptions by considering a static (but rotating) axisymmetric system of collisionless particles, which could for example be a large collection of gravitating stars (a galaxy). The result is the following set of integro-differential equations for the four components \(\nu, B, \mu, \omega\) of the (simplified) metric \(g_{ab}\),

where the right-hand side integrals are given by
![]()
We discretize the left-hand side using the finite element method (FEM) and compute the integrals by numerical quadrature. The nonlinear system is solved by fixed-point iteration in combination with normalization (of the total mass) in each iteration, together with some Anderson acceleration to improve convergence.
Our model has two central parameters, \(L_0\) which is the minimum angular momentum of the particles and \(E_0\) which is the maximum energy of the particles in the system. By carefully tuning these parameters (path-following), we are able to find different regimes that exhibit some quite interesting features. In particular, we believe we are able to construct paths towards both (Kerr) black holes and cosmic strings. Another interesting feature is the formation of ergoregions forming around the support of the matter (see paper for details).
In future work, we will explore whether we can use the Kerr black hole limit to create worm holes and whether we can extract energy from our ergoregions. Stay tuned! 🙂
For now, enjoy these animations illustrating the path-following fixed-point iteration converging to the cosmic string limit for decreasing particle energy \(E_0\).