Mesh generation in FEniCS

FEniCS comes with built-in mesh generation that allows relatively complex domains to be defined and meshed using simple Python code. The meshing capabilities of FEniCS are handled by the (optional) FEniCS component mshr and the actual meshing is performed by CGAL or Tetgen. The interface is inspired by that of Netgen in that domains are defined in terms of Constructive Solid Geometry (CSG).

For example, here’s how to create a mesh of the Death Star in FEniCS:

from fenics import *
from mshr import *
from math import pi, sin, cos, sqrt

# Parameters
R = 1.1
r = 0.4
t = 10
x = R*cos(float(t) / 180 * pi)
y = 0
z = R*sin(t)

# Create geometry
s1 = Sphere(Point(0, 0, 0), 1)
s2 = Sphere(Point(x, y, z), r)
b1 = Box(Point(-2, -2, -0.03), Point(2, 2, 0.03))
geometry = s1 - s2 - b1

# Create mesh
mesh = generate_mesh(geometry, 32)

mshr is the work by my student Benjamin Kehlet who has done a great job with designing an intuitive interface and handling corner cases, cleanups of geometries and various other issues that must be handled to deliver a smooth user experience. A feature that he recently added is the ability to define subdomains as part of domains and meshes. The following code taken from the upcoming FEniCS tutorial illustrates how to define subdomains in a mesh, here for a 2D cross-section of an iron cylinder with a coppper wire wound 10 times around the cylinder:

from fenics import *
from mshr import *
from math import sin, cos, pi

a = 1.0   # inner radius of iron cylinder
b = 1.2   # outer radius of iron cylinder
c_1 = 0.8 # radius for inner circle of copper wires
c_2 = 1.4 # radius for outer circle of copper wires
r = 0.1   # radius of copper wires
R = 5.0   # radius of domain
n = 10    # number of windings

# FIXME: Use 'domain' instead of 'geometry' in other examples

# Define geometry for background
domain = Circle(Point(0, 0), R)

# Define geometry for iron cylinder
cylinder = Circle(Point(0, 0), b) - Circle(Point(0, 0), a)

# Define geometry for wires (N = North (up), S = South (down))
angles_N = [i*2*pi/n for i in range(n)]
angles_S = [(i + 0.5)*2*pi/n for i in range(n)]
wires_N = [Circle(Point(c_1*cos(v), c_1*sin(v)), r) for v in angles_N]
wires_S = [Circle(Point(c_2*cos(v), c_2*sin(v)), r) for v in angles_S]

# Set subdomain for iron cylinder
domain.set_subdomain(1, cylinder)

# Set subdomains for wires
for (i, wire) in enumerate(wires_N):
    domain.set_subdomain(2 + i, wire)
for (i, wire) in enumerate(wires_S):
    domain.set_subdomain(2 + n + i, wire)

# Create mesh
mesh = generate_mesh(domain, 32)

The following plot shows a detail of the mesh. The circles representing cross-sections of the copper wire are clearly visible, as is the outline of the iron cylinder.

The subdomain information is carried over to the FEniCS mesh and can be used to define variational problems, set boundary conditions etc. Here’s a code snippet illustrating how to extract the subdomain data and use it for defining measures for the different subdomains:

# Define subdomain markers and integration measure
markers = MeshFunction('size_t', mesh, 2, mesh.domains())
dx = Measure('dx', domain=mesh, subdomain_data=markers)

# Define current densities
J_N = Constant(1.0)
J_S = Constant(-1.0)

# Define magnetic permeability
class Permeability(Expression):
    def __init__(self, mesh, **kwargs):
        self.markers = markers
    def eval_cell(self, values, x, ufc_cell):
        if markers[ufc_cell.index] == 0:
            values[0] = 4*pi*1e-7 # vacuum
        elif markers[ufc_cell.index] == 1:
            values[0] = 1e-5      # iron (should really be 2.5e-1)
        else:
            values[0] = -6.4e-6   # copper

mu = Permeability(mesh, degree=1)

# Define variational problem
A_z = TrialFunction(V)
v = TestFunction(V)
a = (1 / mu)*dot(grad(A_z), grad(v))*dx
L_N = sum(J_N*v*dx(i) for i in range(2, 2 + n))
L_S = sum(J_S*v*dx(i) for i in range(2 + n, 2 + 2*n))
L = L_N + L_S

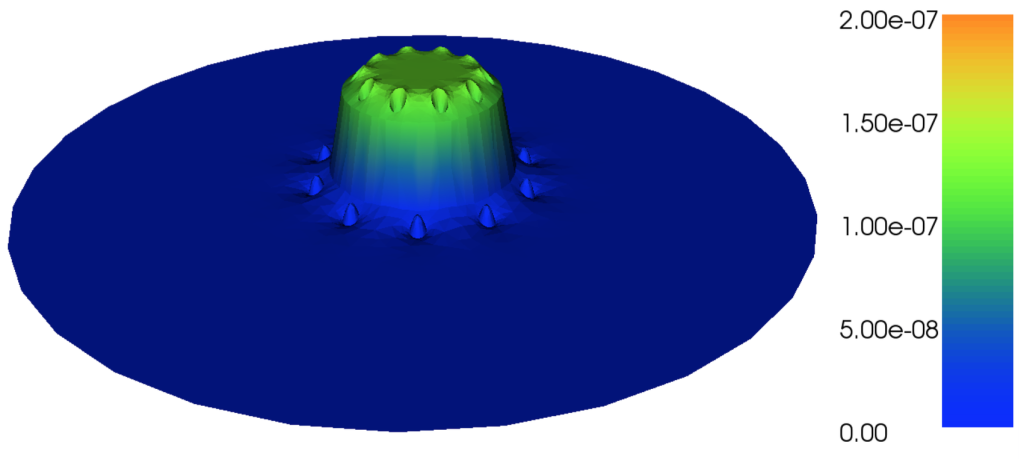
Finally, calling `solve(a == L)` in FEniCS gives us the solution. The plots below show the (z-component of the) magnetic vector potential and the magnetic field.