Here’s a sample from the upcoming FEniCS Tutorial that I’m currently working on with Hans Petter Langtangen. As a simple demonstration of how complex problems can be solved with a minimal amount of code in FEniCS, we simulate a system of chemical reactions taking place in a channel with the flow governed by the incompressible Navier-Stokes equations. The reaction itself is modeled as a first-order reaction using the standard advection-diffusion-reaction equation:

For the velocity field, we use a previously computed solution of the incompressible Navier-Stokes equations which we can read/write using a FEniCS `TimeSeries`. The variational problem for the equations themselves are easily implemented in FEniCS:

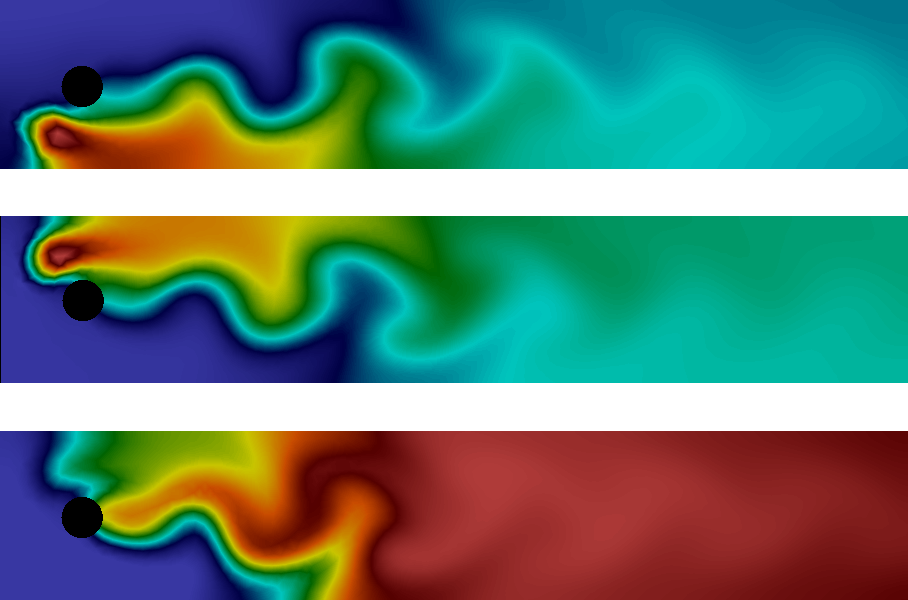
The solution is a quite beautiful wavelike pattern as illustrated in the following clip which plots the concentrations of the three species.
The complete code for the above simulation looks as follows.
from fenics import *
T = 5.0 # final time
num_steps = 500 # number of time steps
dt = T / num_steps # time step size
eps = 0.01 # diffusion coefficient
K = 10.0 # reaction rate
theta = 1.0 # implicitness parameter for time-stepping
# Read mesh from file
mesh = Mesh('channel.xml.gz')
# Define function space for velocity
W = VectorFunctionSpace(mesh, 'P', 2)
# Define function space for system
P1 = FiniteElement('P', 'triangle', 1)
element = MixedElement([P1, P1, P1])
V = FunctionSpace(mesh, element)
# Define test functions
v_1, v_2, v_3 = TestFunctions(V)
# Define functions for velocity and concentrations
w = Function(W)
u = Function(V)
u_p = Function(V)
# Split system functions to access components
u_1, u_2, u_3 = split(u)
u_p1, u_p2, u_p3 = split(u_p)
# Define source terms
f_1 = Expression('pow(x[0]-0.1, 2) + pow(x[1]-0.1, 2) < 0.05*0.05 ? 0.1 : 0',
degree=1)
f_2 = Expression('pow(x[0]-0.1, 2) + pow(x[1]-0.3, 2) < 0.05*0.05 ? 0.1 : 0',
degree=1)
f_3 = Constant(0)
# Define expressions used in variational forms
U_1 = (1 - Constant(theta))*u_p1 + Constant(theta)*u_1
U_2 = (1 - Constant(theta))*u_p2 + Constant(theta)*u_2
U_3 = (1 - Constant(theta))*u_p3 + Constant(theta)*u_3
k = Constant(dt)
K = Constant(K)
eps = Constant(eps)
# Define variational problem
F = ((u_1 - u_p1) / k)*v_1*dx + dot(w, grad(U_1))*v_1*dx \
+ eps*dot(grad(U_1), grad(v_1))*dx + K*U_1*U_2*v_1*dx \
+ ((u_2 - u_p2) / k)*v_2*dx + dot(w, grad(U_2))*v_2*dx \
+ eps*dot(grad(U_2), grad(v_2))*dx + K*U_1*U_2*v_2*dx \
+ ((u_3 - u_p3) / k)*v_3*dx + dot(w, grad(U_3))*v_3*dx \
+ eps*dot(grad(U_3), grad(v_3))*dx - K*U_1*U_2*v_3*dx + K*U_3*v_3*dx \
- f_1*v_1*dx - f_2*v_2*dx - f_3*v_3*dx
# Create time series for reading velocity data
timeseries_w = TimeSeries(mpi_comm_world(), 'ns/velocity')
# Create VTK files for visualization output
vtkfile_u_1 = File('reaction_system/u_1.pvd')
vtkfile_u_2 = File('reaction_system/u_2.pvd')
vtkfile_u_3 = File('reaction_system/u_3.pvd')
# Create progress bar
progress = Progress('Time-stepping')
set_log_level(PROGRESS)
# Time-stepping
t = 0
for n in xrange(num_steps):
# Update current time
t += dt
# Read velocity from file
timeseries_w.retrieve(w.vector(), t - (1.0 - theta)*dt)
# Solve variational problem for time step
solve(F == 0, u)
# Plot solution
_u_1, _u_2, _u_3 = u.split(deepcopy=True)
plot(_u_1, title='u_1', key='u_1')
plot(_u_2, title='u_2', key='u_2')
plot(_u_3, title='u_3', key='u_3')
# Save solution to file (VTK)
vtkfile_u_1 << _u_1
vtkfile_u_2 << _u_2
vtkfile_u_3 << _u_3
# Update previous solution
u_p.assign(u)
# Update progress bar
progress.update(t / T)
# Hold plot
interactive()
Nicholas Danes May 31, 2016
Hi Dr. Logg,
Will there any future documentation with these sorts of problems (systems of ADR equations) with possible stabilization techniques (e.g. SUPG, FEM-FCT, Upwind DG, and/or SOLD methods)?
My own research uses FEniCS and proper stabilization of these sort of problems has been an issue for myself for the past year (in particular, with positivity perservation of ADR equations). I’ve implemented the FEM-FCT method in my personal code, but it does not play well with the native MPI support nor does it scale with systems of ADR equations. I would like eventually to have complete parallel support in my own research code.
Thanks for all you do for this project!
Best,
Nicholas
logg June 2, 2016 — Post Author
There are already a number of demos distributed as part of FEniCS. Perhaps there will be a chapter on stabilized finite element methods in the second volume of the tutorial.
Hossein October 4, 2016
Dear Anders,
When I run the above code I get the following error:
V = FunctionSpace(mesh, element)
TypeError: __init__() takes at least 4 arguments (3 given)
could you please help with this?
Best,
Hossein
logg October 4, 2016 — Post Author
You must be running an old version of FEniCS. Get the latest = v2016.1!
Hossein October 5, 2016
Thanks.
I updated the FEniCS but, again it did not work. I’m using ubuntu 14.04 and version of python is 2.7.6. Are these OK ?
Thank you for your time.
Best,
Hossein
Hossein October 5, 2016
Also version of FEniCS is now 1.6.0
Hossein October 5, 2016
I also tried
element = (P1 * P1) * P1
element = P1 * P1* P1
element = VectorElement(’P’, ’triangle’, 1, dim=3)
but again, I get the same error !
logg October 5, 2016 — Post Author
You should get version 2016.1, not 1.6.0.
Hossein October 5, 2016
Thanks.
It works!